Fizik Deneyleri Laboratuvar Föyü
Harran Üniversitesi Fizik Bölümü
Hazırlayan: Yrd. Doç. Dr. İlker Can ÇELİK
Deney Araçları ve Açıklamaları:
1. Rastlantısal ve Sistematik Hatalar 2. Kumpas 3. Mikrometre 4. Multimetre 5. Hareket
Deney Hataları
Belirsizlik olarak hatalar:
Hata analizine başlamadan önce, hatanın bilimde ne anlama geldiğini öğrenmek gerekir. Hata bilimsel anlamda, yapılan yanlış anlamına gelmez. Aksine, kaçınılmaz olarak oluşan ölçümlerdeki netsizliktir. Mutlaka, yapılan her ölçümde hata yoktur. Örneğin, şu anda odada kaç kişi var diye sorulduğunda, kolaylıkla cevap verebiliriz. Buna rağmen, aynı odada kaç tane atom var diye sorulduğunda (aşağıdaki animasyonu inceleyiniz), tam olarak cevap vermek imkansızlaşır.

Bazı Genel Tanımlar:
İsabetlilik (Accuracy): Ölçülen deneysel değerin gerçek değere yakınlık derecesidir. Daha çok sistematik hatalara atfen kullanılır.
İsabette veya Ölçümde Kesinlik (Precision): Ölçülen değerlerin birbirlerine yakınlık veya tekrarlama derecesidir. Belirli bir tip deneydeki raslantısal hata dağılımına atfen kullanılır.
| low-accuracy-hi-precision | hi-accuracy-low-precision | hi-accuracy-hi-precision |
 |
 |
 |
Örneğin, eğer bir futbolcu daima penaltıda topu sol direğe nişanlıyorsa, bu fotbolcu gol yapma açısından isabetli değildir ama her defasında aynı yere atma konusunda tam bir netlik içindedir.
Çarpıklık (Bias): Eğer ölçümde bir sistematik hata varsa, her defasında aynı sonucu buluruz. Ama bu, bulduğumuz sonucun doğru olduğu anlamına gelmemelidir. Sistematik bir hata olması durumunda, bulunan bütün cevaplar aslında yanlıştır. Bu yüzden aletlerimizin kullanılmadan önce kalibre edilmesine dikkat etmeliyiz.
Örneğin, tartımızın üstünde birşey yokken bile 1 kg göstermesi, boyumuzu giyerken ayakkabı giymemiz, durması için 1 saniyeye ihtiyaç suyan bir kronometre hep bu türden hatalara örnektir.
Ölçümde isabetliliğin derecesi (The degree of accuracy): Ölçülen birim aralığının göstergedeki değerinin, her iki yandan yarısı kadar gidilirse; ölçğlen değer göstergedeki değerin kendisi olacaktır. Bunu aşağıdaki bir örnekle açıklayıp netleştirelim.
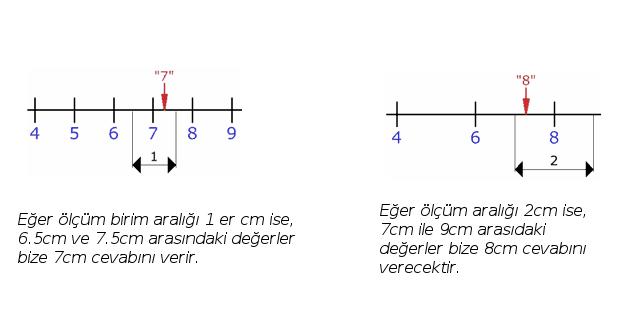
Ölçümdeki çözünürlük (Measurement resolution): Ölçümde isabetlilik ve kesinliğin dışında birde aletimizle ölçülebilecek en ufak fiziksel değişime aletimizin çözünürlüğü denir.
Sistematik Hatalar:
Deneylerdeki gözlemlerde, sistematik hatalar ölçüm yapılan aletten ileri gelir. Oluşma nedenleri ise:
1. Ölçüm aletindeki içsel hatadan dolayı veya ondaki data analiz etme yöntemindeki yanlışlıktan,
2. veya deney yapan kişinin deneyi tam anlamıyla doğru yapamamasından ileri gelir.
Lineer olarak cevap veren ölçüm aletinde iki tip sistematik hata oluşabilir:
1. Offset (başlangıcın orjine denk gelmemesi) veya sıfırı gösterme ayarı hatası diyede bilinen hatada, ölçüm aleti ölçülen değer sıfır olmasına rağmen sıfırı göstermez.
2. Çarpım veya skala faktörü hatası da denilen hatada ise, alet sürekli olarak okunması gereken ölçümden ya küçük yada büyük değeri ölçmektedir.
Hata türlerinin gösterimi:

Sistematik hatalar, linear ölçüm yapmayan aletlerde kalibrasyondan doğan sebep ötürü de oluşabilir
Üstünde çalışılan aletin yanlış kullanımından kaynaklanan sistematik hata örnekleri:
1. Termometre ve sicaklığı ölçülecek madde arasındaki yalıtım veya zayıf termal ısı iletimi sorunu yüzünden ölçülen sıcaklık hataları.
2. Güneş ışını radyasyonu ölçümünün, ölçü aletinin gölgede kalmasına neden olan binalar ve ağaçlar yüzünden yanlış okunması.
Raslantısal Hatalar:
Rastlantısal hatalar, deneydeki bilinmeyen veya önceden tahmin edilemeyen değişiklikler tarafından ortaya çıkar. Bu hatalar ya kullanılan alette ya da deney ortamında oluşmuş olabilir.
Rastlantısal hatalara sebep olabilecek örnekler:
1. Elektriksel aletteki arka planda oluşan ve elektriksel gürültü (electronic noise) denen etki.
2. Rüzgardaki değiklikten ötürü, ısı toplayıcıdaki ısı kaybı oranındaki düzensiz değişiklikler.
Rastlantısal hatalar genellıkle matematikte "Gaus normal dağılım fonksyonu" şeklindeki bir yayılma gösterir. Bu durumda, istatistiksel metodlar veri analizinde devreye girecektir. Şimdi "Gaus dağılım fonksiyonunun" formüle edilişini, taşıdığı parametreleri ve fonksiyonunun istatistiksel olarak ne ifade ettiğini görelim.
Burada "a" harfi Gaus eğrisinin max yüksekliğini, "x̄" pik merkezinin x ekseni üzerindeki yerini, "σ" ise standart sapma değerini göstermektedir. Gaus grafiğinin şekli karakteristik simetrik "çan eğrisi (bell curve)" şeklindedir. Standart sapma, gaus eğrisinin genişliğini kontrol eden parameteredir. FWHM değeri gaus eğrisi için 2,35σ ya eşittir. FWHM, eğrinin yarı yüksekliğindeki genliğidir.
Standart Sapma Hesabı:
| basit sarkaç | kronometre |
 |
 |
Örneğin, basit bir sarkacın salınım sürelerini birkaç kere kronometre ile ölçtüğümüzüz varsayalım. Bu ölçümlerde tam bir tutarlılık olmayacaktır. Fakat, yapılan ölçüm sayısı arttıkça, asıl değere daha da yaklaşılacaktır.
| Deneme Sırası=xi | 1 | 2 | 3 | 4 | 5 |
| Ölçülen değer (s)=x | 3.9 | 3.5 | 3.7 | 3.4 | 3.5 |
| Sapma miktarı (s)=xi-x̄ | 0.3 | -0.1 | 0.1 | -0.2 | -0.1 |
Ölçülen bu 5 değer için bulunan en iyi tahmin ortalama değer olan gelen 3.6 saniye olacaktır. Burada "N" kaç tane değer girildiğini göstermektedir. Şimdi, ilk akla gelen şeylerden bir tanesi, maximum sapmayı gösteren 0.3 saniye değerini kullanıp, kendimizi garantiye almak olabilir. Fakat, bu yöntemde yanlış olan şey, hata payını fazla tahmin etmektir. Aynı zamanda, bizi ilgilendiren aslında ortalama sapma değeri olmalıdır.
Bu ifaden de anlaşılacağı üzere standart sapmaların ortalamasını kullanmak pek akla yatkın değildir.
Öyleyse, birde bu ifadeyi deneyelim. σ2x= 1⁄ N ∑ d2i= √[(0.09+0.01+0.01+0.04+0.01)⁄5]= 0.2 saniye .
Dolayısıyla, bu basit sarkacın tam devir için gereken periyot süresi T=x̄+/-σx
Website Stats